Великдень у християнських церквах східного (православ’я) та західного обряду (католицизм) святкується в першу неділю після весняної повні (повного місяця), але як би це парадоксально не звучало, тут є математика!
При цьому весняна повня – це перший повний місяць, що настає не раніше, ніж день весняного рівнодення. Причина відносної складності обчислень полягає у тому, що потрібно узгодити між собою сонячний і місячний календарі, а також взяти до уваги той факт, що Великдень припадає на фіксований день тижня, тобто на неділю. У церквах східного обряду ще потрібно взяти до уваги різницю між Григоріанським та Юліанським календарями (у 21-му столітті вона складає 13 днів).
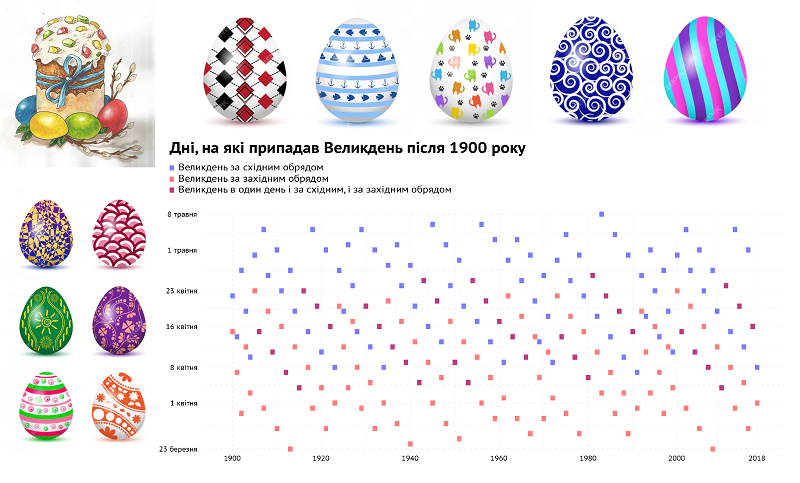
Якщо ми поглянемо на дати Великодня з 1900 року, то важко не помітити певну циклічність у датах свята. При цьому циклічними є і збіги обох Великоднів (всього таких було 37.7%).
У 1800 році 23-річний математик Карл Фрідріх Гаусс побачив у визначенні дати Великодня цікаве рівняння, яке враховує цикли переміщень сонця і місяця та особливості календарної системи і вперше представив алгоритм для обчислення Великодня за старим та новим стилем. Через 16 років один з його студентів виявив помилку у алгоритмі та разом з Гауссом виправив її.
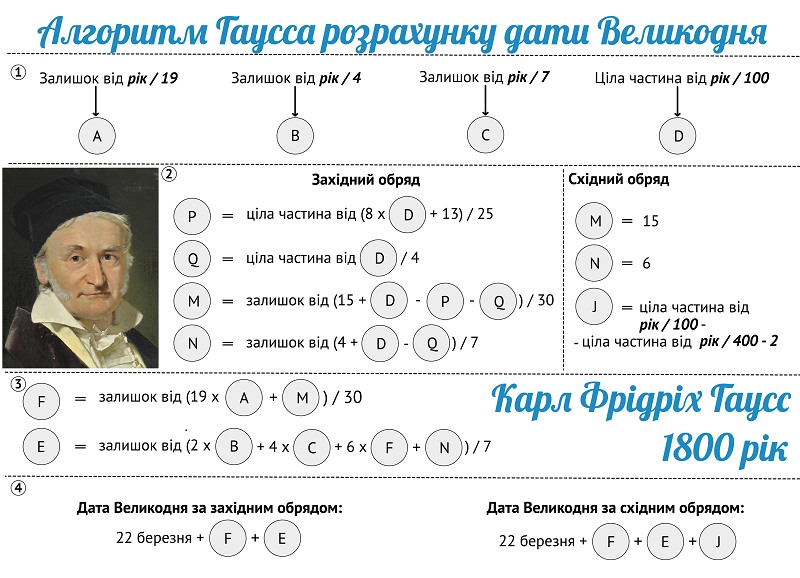
Розрахунок дати православного Великодня 2025 року:
- Визначаємо A – залишок від ділення року на 19 (2025 mod 19):
2025 ÷ 19 = 106 з залишком A=11
- Визначаємо B – залишок від ділення року на 4 (2025 mod 4):
2025 ÷ 4 = 506 з залишком B=1
- Визначаємо C – залишок від ділення року на 7 (2025 mod 7):
2025 ÷ 7 = 289 з залишком C=2
- Визначаємо D – цілу частину від ділення року на 100:
2025 ÷ 100 = 20 (D=20)
- M = 15
- N = 6
- Обчислюємо J (різницю між Григоріанським та Юліанським календарями) – це різниця цілої частини від ділення року на 100 мінус ціла частина від ділення року на 400 мінус 2:
2025 ÷ 100 – 2025 ÷ 400 – 2 = 20 – 5 – 2 = 13
- Обчислюємо F = (19 × A + M) mod 30 = (19 × 11 + 15) mod 30 = (209 + 15) mod 30 = 224 mod 30 = 14
- Обчислюємо E = (2 × B + 4 × C + 6 × F + N) mod 7 = (2 × 1 + 4 × 2 + 6 × 14 + 6) mod 7 = (2 + 8 + 84 + 6) mod 7 = 100 mod 7 = 2
Визначаємо дату Великодня:
22 березня + F + E + J = 22+14+2+13 = 51 день від початку березня.
Оскільки в березні 31 день, 51 – 31 = 20, тому дата випадає на 20 квітня.
Отже, за східним (православним) обрядом Великдень у 2025 році припадає на 20 квітня.
Розрахунок дати католицького Великодня 2025 року:
- Визначаємо A – залишок від ділення року на 19 (mod 19):
2025 ÷ 19 = 106 з залишком A=11
- Визначаємо B – залишок від ділення року на 4 (mod 4):
2025 ÷ 4 = 506 з залишком B=1
- Визначаємо C – залишок від ділення року на 7 (mod 7):
2025 ÷ 7 = 289 з залишком C=2
- Визначаємо D – цілу частину від ділення року на 100:
2025 ÷ 100 = 20 (D=20)
- Визначаємо P – цілу частину від (8 × D + 13) ÷ 25:
(8 × 20 + 13) ÷ 25 = (160 + 13) ÷ 25 = 173 ÷ 25 = 6 (P=6)
- Визначаємо Q – цілу частину від D ÷ 4:
20 ÷ 4 = 5 (Q=5)
- Обчислюємо M = (15 + D – P – Q) mod 30 = (15 + 20 – 6 – 5) mod 30 = 24 mod 30 = 24
- Обчислюємо N = (4 + D – Q) mod 7 = (4 + 20 – 5) mod 7 = 19 mod 7 = 5
- Обчислюємо F = (19 × A + M) mod 30 = (19 × 11 + 24) mod 30 = (209 + 24) mod 30 = 233 mod 30 = 23
- Обчислюємо E = (2 × B + 4 × C + 6 × F + N) mod 7 = (2 × 1 + 4 × 2 + 6 × 23 + 5) mod 7 = (2 + 8 + 138 + 5) mod 7 = 153 mod 7 = 6
Визначаємо дату Великодня:
22 березня + F + E = 22+23+6 = 51 день від початку березня.
Оскільки в березні 31 день, 51 – 31 = 20, тому дата випадає на 20 квітня.
Отже, католицький Великдень 2025 року також припадає на 20 квітня.
За матеріалами кафедри фізики, математики
та методики навчання
