Якщо вам кажуть, що ви багатогранна особистість – тіштеся, але не дуже. Можливо, мається на увазі що ви пияка, мерзотник і свиня водночас)
Минулого разу ми розглянули захопливий світ сучасної математики, що стоїть за кожним пошуковим запитом у Google, а сьогодні знов повертаємось до математичних проблем століття в цілому і до 3-ї проблеми Гільберта зокрема!
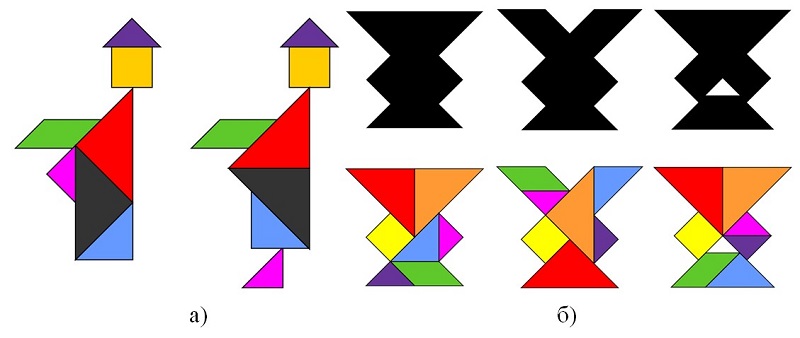
У черговий раз у межах роботи математичного гуртка факультету ФМКТО БДПУ (наразі вже загальноуніверситетського!) відбулося захопливе заняття, яке поєднало здобувачів освіти з навчанням на перетині геометрії, головоломок і математичної краси теорем. Учасники поринули у світ рівноскладеності, конгруентності та магічної симетрії фігур, досліджуючи давні та сучасні головоломки – танграм, Остомахіон, Т-головоломку тощо.
Окрема дискусія була присвячена поняттю конгруентності – геометричній рівності фігур за формою і розміром. Під час практичної частини учасники складали фігури з елементів танграму, досліджуючи, як однакові частини можуть утворювати сотні нових форм – тварин, предметів, символів.
Основну увагу було зосереджено на третій проблемі Гільберта, що стосується рівноскладеності многогранників – можливості скласти одну просторову фігуру з частин іншої без зміни об’єму. Здобувачі переглянули анімації та відеоматеріали, які наочно продемонстрували, як на площині квадрат можна розкласти і скласти у правильний шестикутник тієї ж площі, а куля у просторі рівноскладена двом своїм копіям! Це викликало справжній подив і зацікавлення.
Заняття продемонструвало, як глибокі математичні ідеї можуть оживати у вигляді простих і цікавих головоломок. Отримані математичні знання стали не просто абстракцією, а інструментом творчості та гри. Такі зустрічі допомагають не лише зрозуміти математику, але й побачити її красу.

За матеріалами кафедри фізики, математики та методики навчання

