Одного разу вчитель запитав майбутнього великого грецького математика Евкліда:
— Що б ти вибрав: два цілих яблука чи чотири їхні половинки?
— Звісно, чотири половинки.
— А чому? — запитав вчитель.
— Адже це одне й те саме.
— І зовсім не одне й те саме, — відповів майбутній математик.
— Вибравши два цілих яблука, як я зміг би дізнатися, червиві вони чи ні?..
Минулого разу ми розглянули математичний доробок Піфагора Самоського – математика, філософа, містика і творця однієї з найвідоміших теорем в історії людства, а сьогодні повернулися до самих витоків геометричної думки, щоб торкнутися вічної мудрості Евкліда Олександрійського!
У черговий раз цього семестру у межах роботи математичного гуртка факультету ФМКТО БДПУ протягом двох тижнів відбулися два захопливі заняття, присвячені «Началам» Евкліда – монументальній праці, що понад два тисячоліття залишається еталоном математичної строгості та логічної досконалості. Учасники поринули у світ античної геометрії, де кожна теорема народжується з п’яти елегантних постулатів, а дедуктивний метод розкриває структуру самого Всесвіту. (https://youtu.be/dY6U-LlRoHc)
Здобувачі освіти дізналися про славнозвісний п’ятий постулат про паралельні прямі, дискусії навколо якого згодом породили неевклідові геометрії та революціонізували наше розуміння Всесвіту. Учасники навчились бачити красу дедуктивного методу – як із мінімальних припущень виростає величезна будівля математичних істин.
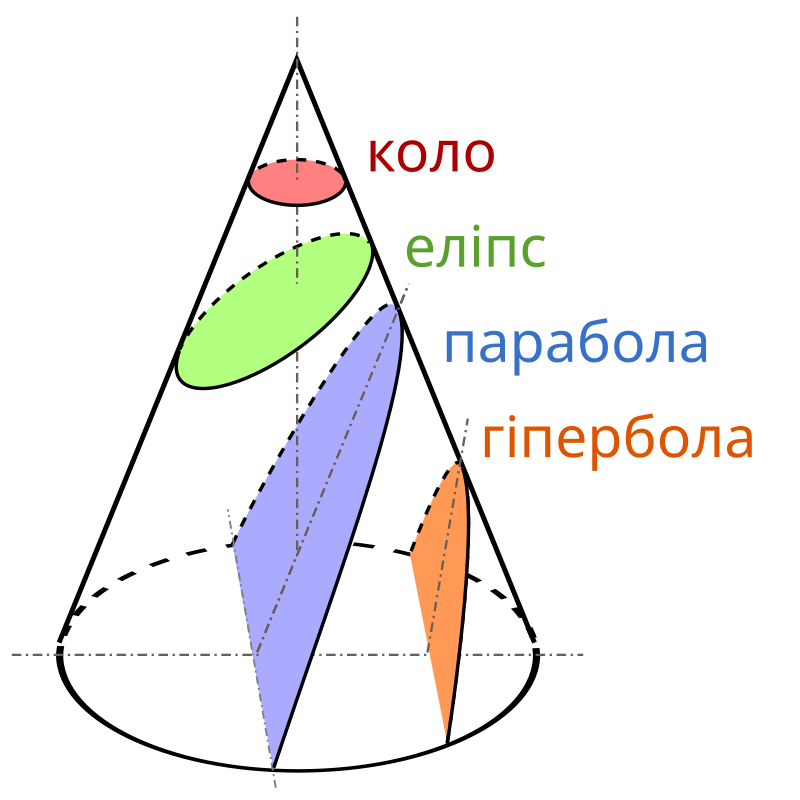
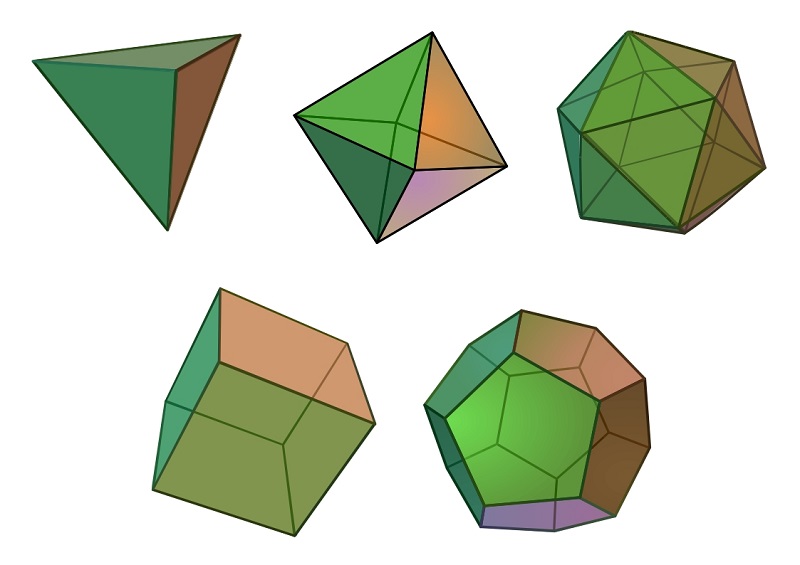
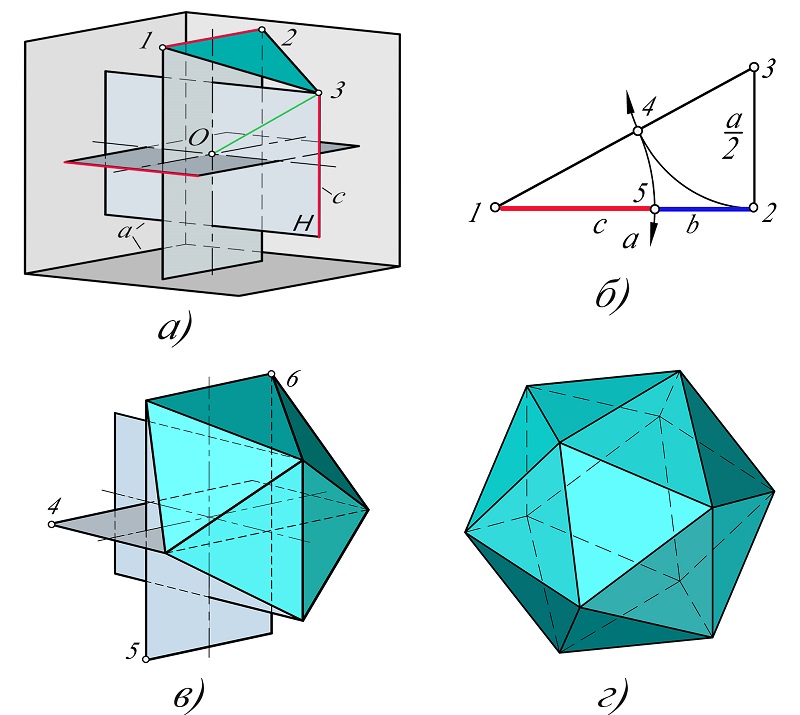
Учасники побачили, як давні математики працювали із золотим перерізом у піфагорейській зірці, досліджували платонові тіла, розгадували таємниці числа π, а також знаходили прості числа решетом Ератосфена і доводили їх нескінченність.
Заняття продемонструвало неймовірний зв’язок між античною мудрістю та сучасною математикою. Здобувачі зрозуміли, що алгоритм Евкліда досі залишається основою комп’ютерних обчислень, піфагорові трійки живуть у криптографії, а танграм та квадратура кола нагадують про вічні питання математичної творчості – ті самі принципи, які вони вивчали на занятті.
Особливо вразило учасників усвідомлення того, що «Начала» Евкліда – це не просто підручник геометрії, а філософія мислення, де кожне твердження випливає з попереднього з незаперечною логікою, де немає місця інтуїції без доведення, а істина народжується лише через строгу аргументацію.
Повна версія:
Цитування: Кудiнов М. П’ять постулатів геометрії Всесвіту: «Начала» Евкліда Александрійського і математика досконалості /М. Кудiнов. — Zenodo. — 2025. — DOI: 10.5281/zenodo.17286062.

За матеріалами кафедри фізики, математики та методики навчання
Five Postulates of the Geometry of the Universe: Euclid of Alexandria’s “Elements” and the Mathematics of Perfection
One day, a teacher asked the future great Greek mathematician Euclid:
— What would you choose: two whole apples or four of their halves?
— Of course, four halves.
— But why? — asked the teacher.
— After all, it’s one and the same.
— And it’s not the same at all, — replied the future mathematician.
— By choosing two whole apples, how could I find out whether they’re wormy or not?..
Last time we examined the mathematical legacy of Pythagoras of Samos – mathematician, philosopher, mystic, and creator of one of the most famous theorems in human history, and today we returned to the very origins of geometric thought to touch upon the eternal wisdom of Euclid of Alexandria!
Once again this semester, as a part of the mathematics club at the Faculty of Physics, Mathematics, Computer Science and Technological Education at BSPU, over the course of two weeks, two captivating sessions took place dedicated to Euclid’s “Elements” – a monumental work that has remained the standard of mathematical rigor and logical perfection for over two millennia. Participants immersed themselves in the world of ancient geometry, where every theorem emerges from five elegant postulates, and the deductive method reveals the structure of the Universe itself. (https://youtu.be/dY6U-LlRoHc)
Students learned about the famous fifth postulate about parallel lines, discussions around which later gave birth to non-Euclidean geometries and revolutionized our understanding of the Universe. Participants learned to see the beauty of the deductive method – how from minimal assumptions grows an enormous edifice of mathematical truths.
Participants saw how ancient mathematicians worked with the golden ratio in the Pythagorean star, explored Platonic solids, unraveled the mysteries of the number π, and also found prime numbers with the Sieve of Eratosthenes and proved their infinity.
The session demonstrated the incredible connection between ancient wisdom and modern mathematics. Students understood that Euclid’s algorithm still remains the foundation of computer calculations, Pythagorean triples live on in cryptography, and the tangram and squaring the circle remind us of eternal questions of mathematical creativity – the very principles they studied during the session.
Participants were especially impressed by the realization that Euclid’s “Elements” is not merely a geometry textbook, but a philosophy of thinking, where each statement follows from the previous one with irrefutable logic, where there is no place for intuition without proof, and truth is born only through rigorous argumentation.
Full version:
Citation: Kudinov M. Five Postulates of the Geometry of the Universe: Euclid of Alexandria’s “Elements” and the Mathematics of Perfection. / M. Kudinov. – Zenodo. – 2025. – DOI: 10.5281/zenodo.17286062





