Чоловік продає собаку.
– У нього величезне генеалогічне дерево!
– А скільки поколінь на ньому позначено?
– На ньому – не знаю, а під ним відзначилися купа поколінь! Он воно у дворі стоїть!
Минулого разу ми за науковою статтею 2021 року заново дослідили знамениту проблему 36 офіцерів Леонарда Ейлера та її розв’язок за латинськими квадратами – математичними структурами, де кожен символ зустрічається рівно один раз у кожному рядку та стовпці, а сьогодні до розгляду – теорія графів!
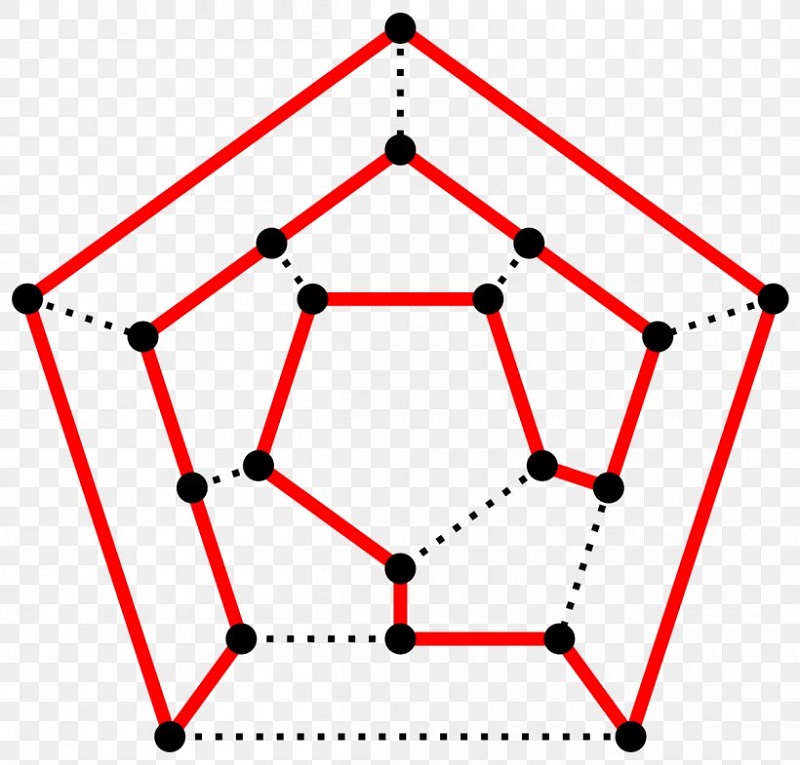
На черговому занятті математичного гуртка факультету ФМКТО БДПУ учасники занурилися в чарівний світ графів – математичних структур, що лежать в основі як старовинних головоломок, так і сучасних технологій.
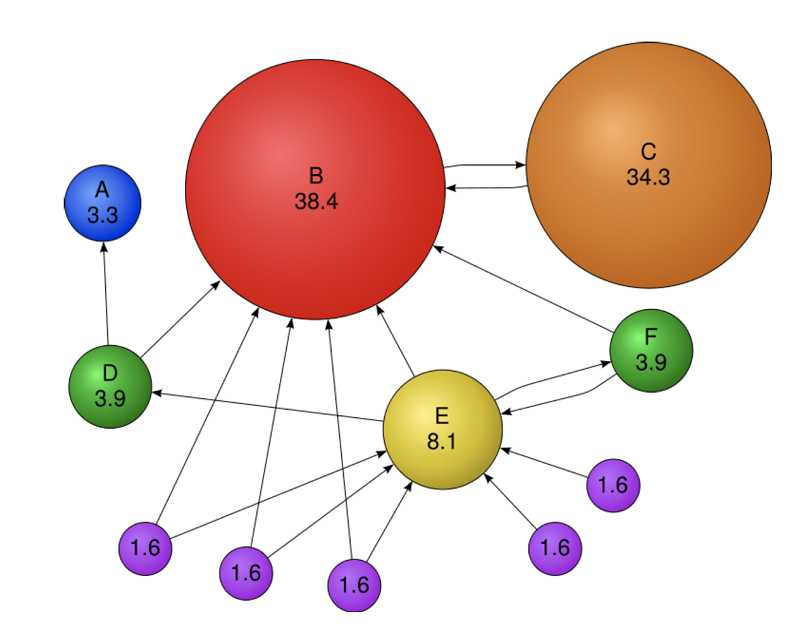
Заняття розпочалося з історії знаменитої задачі про сім мостів Кенігсберга, яку ще у XVIII столітті сформулював Леонард Ейлер – одного з родоначальників теорії графів. Учасники гуртка дізналися, як представити складні системи у вигляді графів, де вершини – це об’єкти, а ребра – зв’язки між ними. Були розглянуті різні типи графів: орієнтовані і неорієнтовані, зважені, дерева та мережі.
Особливу увагу було приділено застосуванню теорії графів у сучасних технологіях. Соціальні мережі, як-от Facebook, використовують графи для моделювання зв’язків між користувачами, що дозволяє створювати алгоритми рекомендацій. А в галузі IT і штучного інтелекту графи допомагають структурувати знання та будувати системи прийняття рішень, знаходять найкоротші маршрути та навіть розпізнають зображення.
Заняття стало справжнім мостом між математичною класикою та інноваціями XXI століття, відкривши гуртківцям нові горизонти знань і надихнувши на подальші дослідження.
За матеріалами кафедри фізики, математикита методики навчання