Один математик питає іншого:
– Скільки буде нескінченність поділити навпіл?
– Нескінченність! – відповідає той.
– Ні! Якщо ділити по горизонталі, то дві трійки, а якщо по вертикалі, то два нулі:)
Протягом двох попередніх занять ми поринули в захопливий світ алгебри і теорії чисел, розкриваючи таємничі взаємозв’язки та дивовижні характеристики цих будівельних цеглинок математичної науки, тож сьогодні постало питання: чи можна за допомогою чисел злічити нескінченність?
На черговому занятті математичного гуртка факультету ФМКТО БДПУ «Чи має нескінченність розмір? Континуум-гіпотеза і готель Гільберта» учасники дослідили (як і свого часу великий математик Георг Кантор) питання про те, чи може існувати множина, потужність якої є більшою за зліченну нескінченність, але меншою за потужність континууму.
На початку заняття гуртківці познайомилися з математичними проблемами тисячоліття, сформульованими Давидом Гільбертом і представленими ним на Міжнародному Конгресі математиків у Парижі в 1900 році. Цікаво, що з цих 23 проблем, які стали дороговказом для розвитку математики XX століття, 16 було розв’язано, ще 2 виявилися некоректно сформульованими, а 5 і до сьогодні залишаються предметом активних досліджень науковців усього світу.
Першою в списку Гільберта з’явилась проблема Кантора про потужність континууму (континуум-гіпотеза), яку й було розглянуто на занятті гуртка. Додаткову увагу ми приділили парадоксу Банаха-Тарського, який демонструє дивовижні властивості нескінченності: як можна «розрізати» кулю на частини та отримати дві кулі такого ж розміру!
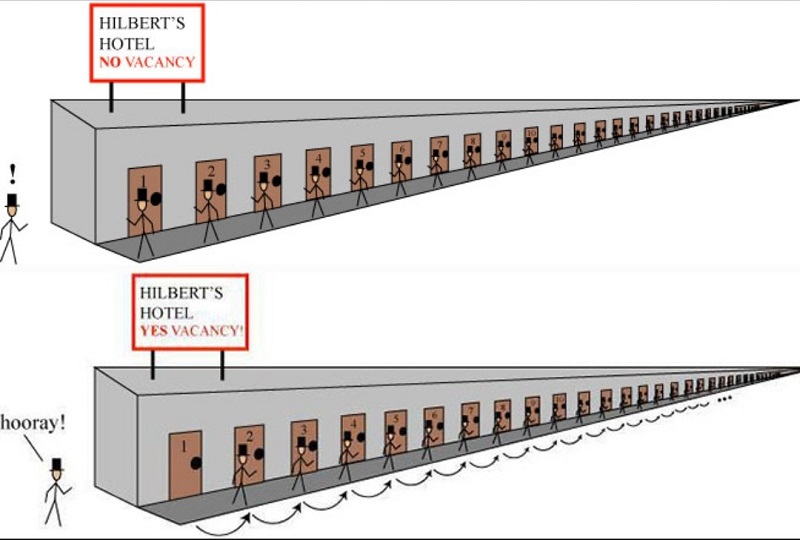
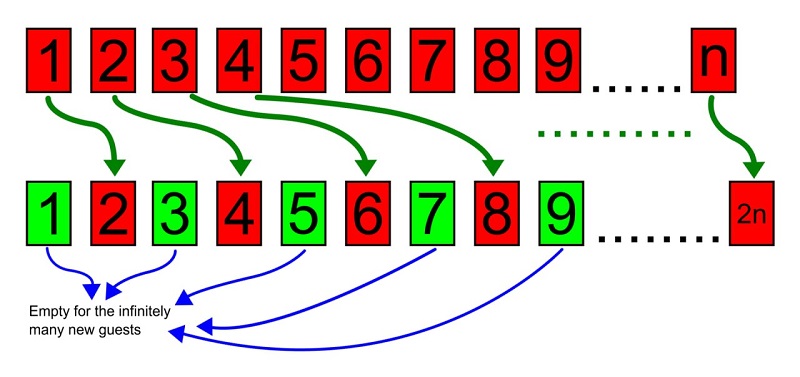
Учасники гуртка дослідили концепцію різних типів нескінченності та порівняли їх, використовуючи наочний приклад «готелю Гільберта» – математичної конструкції, що допомагає зрозуміти властивості нескінченних множин. При застосуванні цієї абстракції нескінченна кількість нових гостей не є перешкодою для їх заселення у повністю заповнений нескінченний готель!
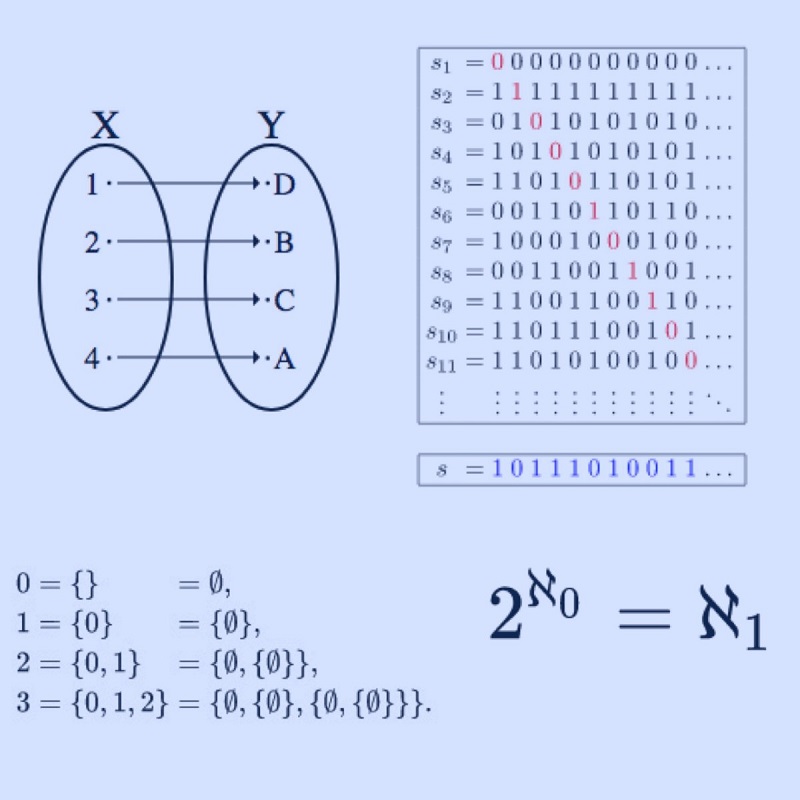
На довершення, як вишенькою на торті, стало знайомство з концепціями «алеф-нуль», «булеан», «омега» і «алеф-1», які показують потужність зліченних і незліченних множин.
Заняття продемонструвало, що математика не лише відкриває дивовижні парадокси, але й будує абстрактні математичні концепції, які допомагають розширити наше розуміння фундаментальних властивостей всесвіту і логіки мислення.




За матеріалами кафедри фізики, математики
та методики навчання

