У раю Архімед, Паскаль та Ньютон грають у хованки. Архімед водить і починає рахувати. Паскаль тікає за обрій, а Ньютон озирається, бере палицю, малює навколо себе квадрат зі стороною 1 метр і стає всередину квадрата. Архімед закінчує рахувати, розплющує очі і бачить Ньютона:
– Я бачу Ньютона!
– Е, ні! Ньютон на квадратний метр – це Паскаль! – відповів той.
Після математичної подорожі до античних Сіракуз, де під впливом Архімеда народилася наука про важелі, спіралі та нескінченність, ми здійснили ще розгляд математичної спадщини Ферма та Лейбніца (про це трохи згодом) і узагальнили античну математику відкритою міжуніверситетською лекцією «Три титани давньогрецької математики».
У черговий раз цього семестру в межах роботи математичного гуртка факультету ФМКТО БДПУ відбулося захопливе заняття у розширеному форматі, присвячене науковій спадщині Ісаака Ньютона – генія, який назавжди змінив наше розуміння Всесвіту. Учасники, серед яких було 5 запрошених учнів Бердянської гімназії «Лідер» разом із вчителем математики Єфімовою Марією Василівною, поринули у світ флюксій та механіки, де математичні формули пояснюють рух планет, падіння яблук і танець світлових променів.
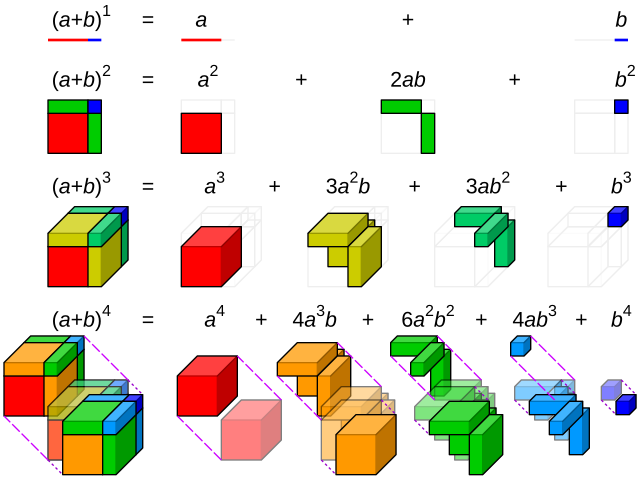
Основну увагу було зосереджено на революційних відкриттях Ньютона: методі флюксій (прообразі диференціального числення) і біномі Ньютона. Здобувачі освіти дізналися, як він відкриває двері до розуміння нескінченних рядів, наближених обчислень і навчились бачити зв’язок між абстрактними математичними конструкціями та фізичними явищами, що оточують нас щодня. Учасники побачили, як Ньютон, описуючи рух, створив принципово нову математичну мову – мову змін, яка сьогодні лежить в основі всієї сучасної фізики та інженерії.
Заняття продемонструвало неймовірний зв’язок між чистою математикою та фізичною реальністю: формула закону всесвітнього тяжіння – це не просто набір символів, а ключ до розуміння космічного порядку, від орбіт супутників до припливів в океанах, керованих тими математичними принципами, які вони вивчали на занятті.

За матеріалами кафедри фізики, математики та методики навчання
The British Father of Mathematical Analysis: Newton’s Binomial Theorem, Gravity, and the Decomposition of Light into Colors

In heaven, Archimedes, Pascal, and Newton are playing hide-and-seek. Archimedes is “it” and starts counting. Pascal runs off beyond the horizon, while Newton looks around, picks up a stick, draws a square with sides of 1 meter around himself, and stands inside the square. Archimedes finishes counting, opens his eyes, and sees Newton:
“I see Newton!”
“Oh no! Newton per square meter is Pascal!” Newton replies.
Following our mathematical journey to ancient Syracuse, where the science of levers, spirals, and infinity was born under Archimedes’ influence (https://news.bdpu.org.ua/arhimedova-syla-uyavy-yak-antychnyj-genij-zvazhuvav-svit-i-obchyslyuvav-neskinchennist/), we also explored the mathematical legacy of Fermat and Leibniz (more on this soon) and summarized ancient mathematics through an open interuniversity lecture “Three Titans of Ancient Greek Mathematics” (https://news.bdpu.org.ua/nauka-i-osvita-ne-zupynyayutsya-vidkryta-mizhuniversytetska-lekcziya-try-tytany-davnogreczkoyi-matematyky/).
Once again this semester, as part of the mathematical club activities at the Faculty of Physics, Mathematics, Computer Science and Technological Education of Berdiansk State Pedagogical University, a fascinating extended-format session was held dedicated to the scientific legacy of Isaac Newton—the genius who forever changed our understanding of the Universe. Participants, including 5 invited students from Berdiansk Gymnasium “Leader” along with their mathematics teacher Maria Vasylivna Yefimova, immersed themselves in the world of fluxions and mechanics, where mathematical formulas explain planetary motion, falling apples, and the dance of light rays.
Primary focus was placed on Newton’s revolutionary discoveries: the method of fluxions (the prototype of differential calculus) and Newton’s binomial theorem. Students learned how it opens doors to understanding infinite series and approximate calculations, and they learned to see the connection between abstract mathematical constructions and the physical phenomena that surround us daily. Participants observed how Newton, in describing motion, created a fundamentally new mathematical language – the language of change – which today underlies all modern physics and engineering.
The session demonstrated the incredible connection between pure mathematics and physical reality: the formula for the law of universal gravitation is not merely a set of symbols, but a key to understanding cosmic order, from satellite orbits to ocean tides, governed by the same mathematical principles they studied during the session.






