Як казав Архімед по п’ятницях – дайте мені склянку віскаря, і я тут усе переверну!!!
Протягом двох попередніх занять ми заглибились у непідвладну часу геометрію «Начал» Евкліда, де кожна теорема народжується з постулатів і аксіом, а сьогодні здійснили математичну подорож до античних Сіракуз, де під впливом Архімеда народилася наука про важелі, спіралі та нескінченність!
У черговий раз цього семестру у межах роботи математичного гуртка факультету ФМКТО БДПУ відбулися три захопливі заняття, присвячені постаті Архімеда, – фізика, математика і винахідника, чиє ім’я стало синонімом геніальності. Учасники поринули у світ науки, де математичні відкриття народжувалися з практичних завдань, а абстрактні ідеї втілювалися у конкретних механізмах.
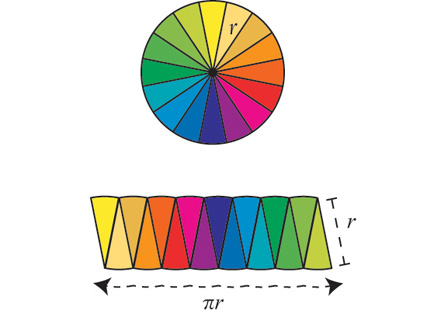
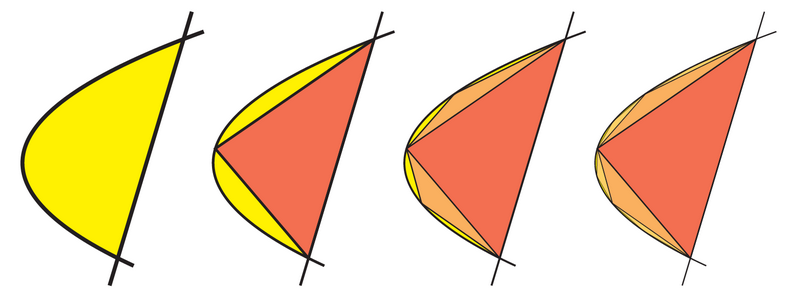
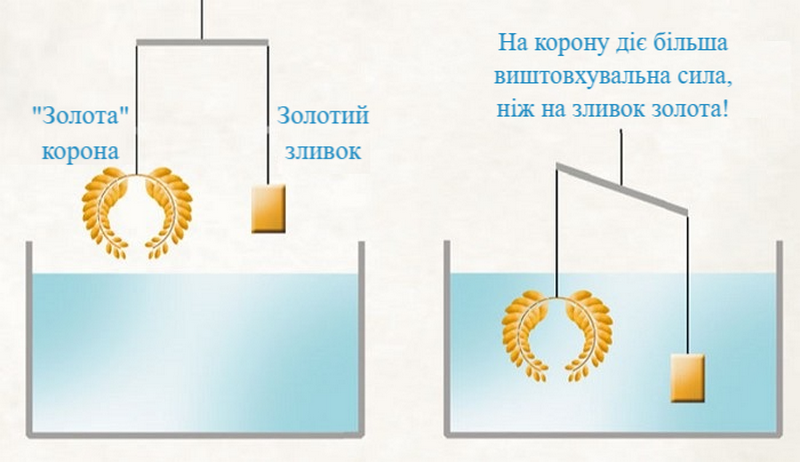
Основну увагу було зосереджено на математичній спадщині Архімеда – від методу вичерпування та квадратури параболи до елегантної спіралі, що носить його ім’я. Здобувачі освіти дізналися про знамениту задачу із золотою короною та відкриття виштовхувальної сили, дослідили геометричну красу арбелоса та салінона, а також навчилися розуміти, як давньогрецький вчений підходив до трисекції кута за допомогою невсиса. Учасники навчились бачити зв’язок між теоретичною математикою та її практичним застосуванням – від важелів, що можуть «перевернути Землю», до обчислення об’ємів складних тіл обертання.
Окрема дискусія була присвячена поняттю нескінченності в античному розумінні, коли Архімед довів, що навіть кількість піщинок, потрібних для заповнення Всесвіту, можна обчислити. Учасники побачили, як давньогрецький математик оперував величезними числами задовго до появи сучасної нотації. Здобувачі зрозуміли, що закон Архімеда, диференціальні залежності та геометричні властивості кіл Аполлонія – це не просто абстрактні теореми, а живі інструменти пізнання, що служать людству вже двадцять три століття.
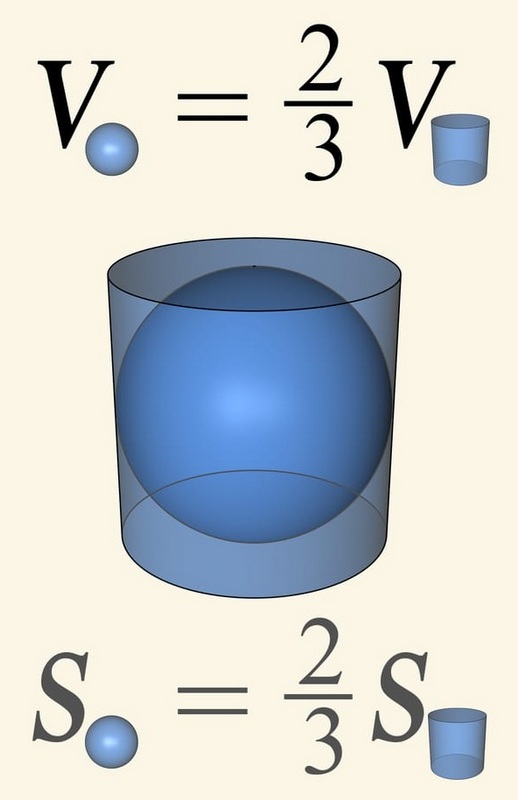
Особливо вразило учасників усвідомлення того, що найбільшим бажанням Архімеда було, щоб на його могилі зобразили кулю, вписану в циліндр – символ його улюбленого відкриття про співвідношення їхніх об’ємів. Заняття не лише показало силу математики у розумінні фізичного світу, а й надихнуло учасників на пошук краси в геометричних побудовах, гармонії у пропорціях і творчості в розв’язанні задач, що здавалися нерозв’язними.
Повна версія:


За матеріалами кафедри фізики, математики та методики навчання
Archimedes’ Force of Imagination: How an Ancient Genius Weighed the World and Calculated Infinity

As Archimedes used to say on Fridays – give me a glass of whiskey, and I’ll turn this whole place upside down!!!
During the two previous sessions, we delved into the timeless geometry of Euclid’s “Elements,” where every theorem is born from postulates and axioms, and today we took a mathematical journey to ancient Syracuse, where under Archimedes’ influence, the science of levers, spirals, and infinity was born!
Once again this semester, within the framework of the mathematical club at the FMCTE faculty of BSPU, three fascinating sessions took place, dedicated to the figure of Archimedes – physicist, mathematician, and inventor, whose name has become synonymous with genius. Participants immersed themselves in a world of science where mathematical discoveries emerged from practical tasks, and abstract ideas were embodied in concrete mechanisms.
The main focus was on Archimedes’ mathematical legacy – from the method of exhaustion and quadrature of the parabola to the elegant spiral that bears his name. Students learned about the famous problem of the golden crown and the discovery of buoyant force, explored the geometric beauty of the arbelos and salinon, and learned to understand how the ancient Greek scientist approached angle trisection using the neusis. Participants learned to see the connection between theoretical mathematics and its practical application – from levers that could “move the Earth” to calculating the volumes of complex solids of revolution.
Another discussion was devoted to the concept of infinity in the ancient understanding, when Archimedes proved that even the number of grains of sand needed to fill the Universe could be calculated. Participants saw how the ancient Greek mathematician operated with enormous numbers long before the appearance of modern notation. Students understood that Archimedes’ law, differential relationships, and geometric properties of Apollonian circles are not just abstract theorems, but living tools of knowledge that have served humanity for twenty-three centuries.
Participants were particularly struck by the realization that Archimedes’ greatest wish was to have a sphere inscribed in a cylinder depicted on his tomb – a symbol of his favorite discovery about the ratio of their volumes. The session not only demonstrated the power of mathematics in understanding the physical world, but also inspired participants to seek beauty in geometric constructions, harmony in proportions, and creativity in solving problems that seemed unsolvable.
Full version:








Based on materials from the Department of Physics, Mathematics and Teaching Methods
